Kevin's Great Big Book of Integers

Chapter 1 grade 7 Integer review
In class we learned about the "zero pair".
A zero pair is when you have a positive and negative which when added create 0.
Another way to explain it is you owing money and you having money. If you owe $1 and you have $1 then it creates 0.
In grade 7 we were given "training wheels" or brackets. This term you wont see brackets as much.

Here are some questions you can try if you don't understand.

-3-(-7) = +4
3 negatives subtracting 7 negatives. You only got 3 negatives that can subtracted, which would leave you with 4 negatives. When subtracting something that isn't there, use a zero pair. (Ryan SJ) So then you add 4 positives to create the zero pair. Now you can subtract the -4 and you will be left with +4.

-3-7 = -10
















(many of you may think to subtract, but if there's no sign then it is automatically addition/positive)
3-7 = -4













3 + 7 = +10
3 positives plus 7 more positives = 10 positives

Great Big Book of Integers part 2
Multiplying Integers
(+3)(+8) When the brackets touch it means they "kiss" or multiply
3(+8) When a bracket is touching a number it also means the same thing

Here are some questions to try!

(+2) x (+3) or 2 Groups (x) of +3
+++ <- Group 1 +++ <- Group 2 ++++++ < onblur="try {parent.deselectBloggerImageGracefully();} catch(e) {}" href="https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjjQHZcFJDcoENvVxKxhJf00YCzrYwPdBWY_TfJsfkKVJpB19ZMDv_B_3CC7X4wSXoOrB_1R1fPqPdPRqfleKxILc3O_3h0QJLkNOr_fbngmgC_Nbp-1WjXTcJ4nJPWNruNJkLmqEkT7O5O/s1600/Integers3.bmp">












(-2) x (+3) or Remove 2 groups of +3 = -6
+++ +++ <= Remove. Left with > ------

(-2) x (-3) = +6 (Remove 2 groups of -3)









The Great Big Book Of Integers Part 3
Dividing Integers

Partitive Division is How many groups of ____ "Go Into" ___?
6÷2 = 3









-6÷(-2) = 3









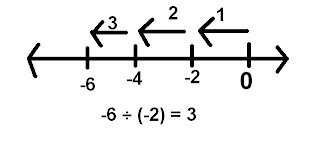
Quotitive Division
Sharing with groups. When both integers are the same(positive/negative) you can use partitive or quotitive division. The will both be positive answers.
Multiplication inverse is another form of writing the same equation.
e.g. 6 ÷ (-2) = -3 or 6 ÷ (-3) = -2

The sign rule is that when there is a even amount of (-) signs its positive.
When there is an odd amount of (-) signs then it will be negative.
If they are the both the same signs, then its positive.

The great big book of integers part 4
Order of operations with integers
I would solve the equation (+5) x (-3) + (-6) ÷ (+3) by using BEDMAS
B.rackets - Start with the brackets and square it up
E.xponents - No exponents so we move to the D
D.ivision - We then divide (-6) by (+3). 6 ÷ 3 = 2 *odd amount of (-) so negative* -2
M.ultiplication - Now we do the multiplication. 5 x 3 = 15 *odd amount (-) so negative* -15
A.ddition - Last mathematical symbol we have is the addition. So add them up!
S.ubtraction - No subtraction signs skip this step.
[(+5) x (-3)] + [(-6) ÷ (+3)] - add the "square brackets"
(-15) + (-2) is the New equation
15 + 2 = 17 *even amount of (-) signs so its positive* +17

STUDY WE ALL HAVE A TEST ON TUESDAY March 22, 2011